Don't forget to set a section icon and cover page (if applicable)
For the copyright notice, make sure to:
Link to the MIT License of this course's GitHub repository. By default, the MIT License links to the Java course repo.
Update the copyright year
Make sure to follow the Course Formatting Guidelines
(Delete the to do list once you're done.)
The Input Layer
Every machine learning model needs to take in a set of inputs. Prior models like linear regression and logistic regression would take numeric inputs and run them through a mathematical expression to derive an output. K-Nearest Neighbors would represent inputs as points in an n-dimensional space. Neural networks, on the other hand, take in inputs through an input layer.
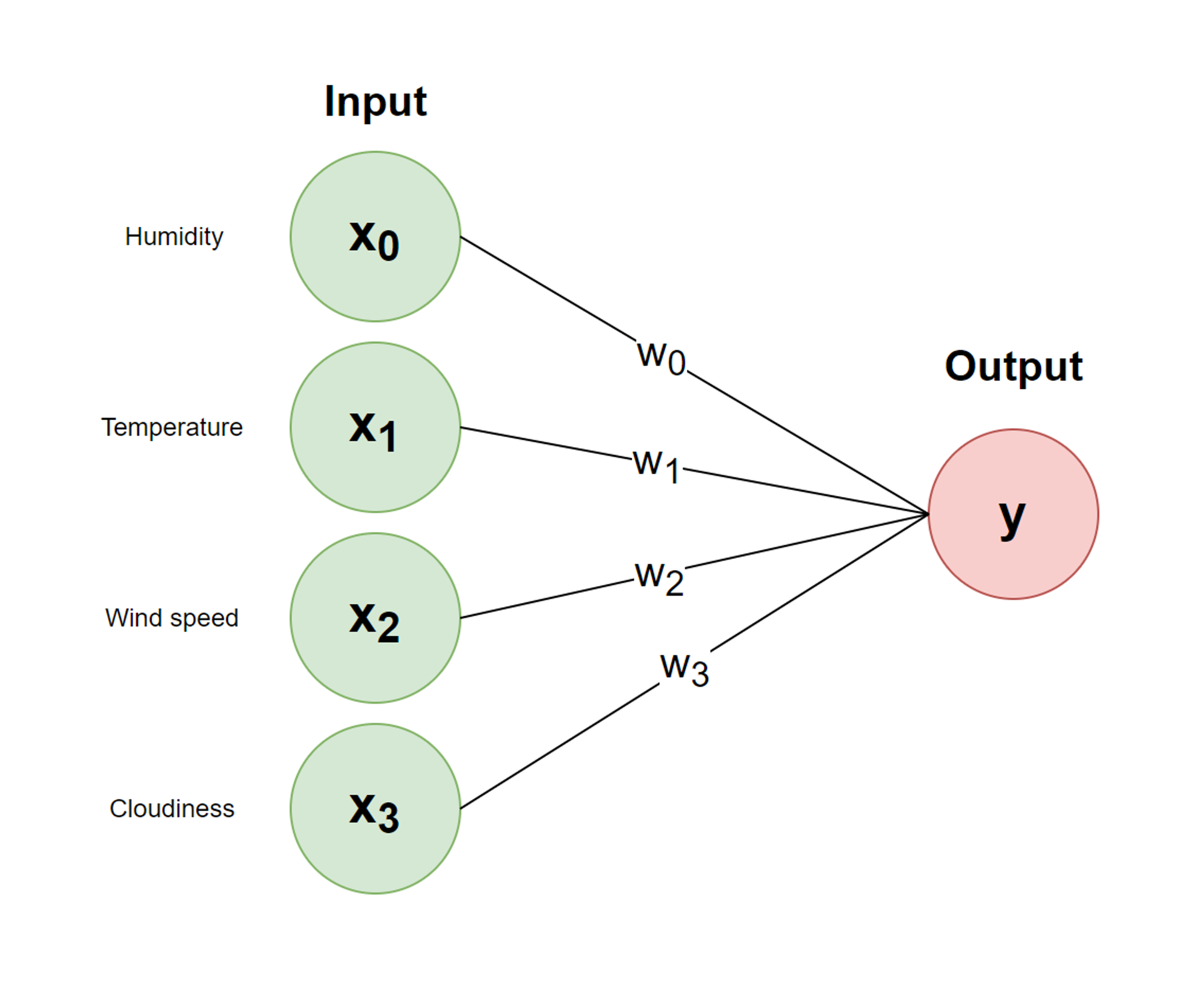
Very generally, the input layer is a set of nodes that take in numeric input. For instance, if we were trying to predict whether it’s raining or not given some information about humidity, temperature, wind speeds, and cloud types, we could designate each input node to one of these values. So, if the humidity was 52%, temperature was 70 degrees F, wind speed was 16 mph, and it was mostly cloudy, the input layer would look something like this:
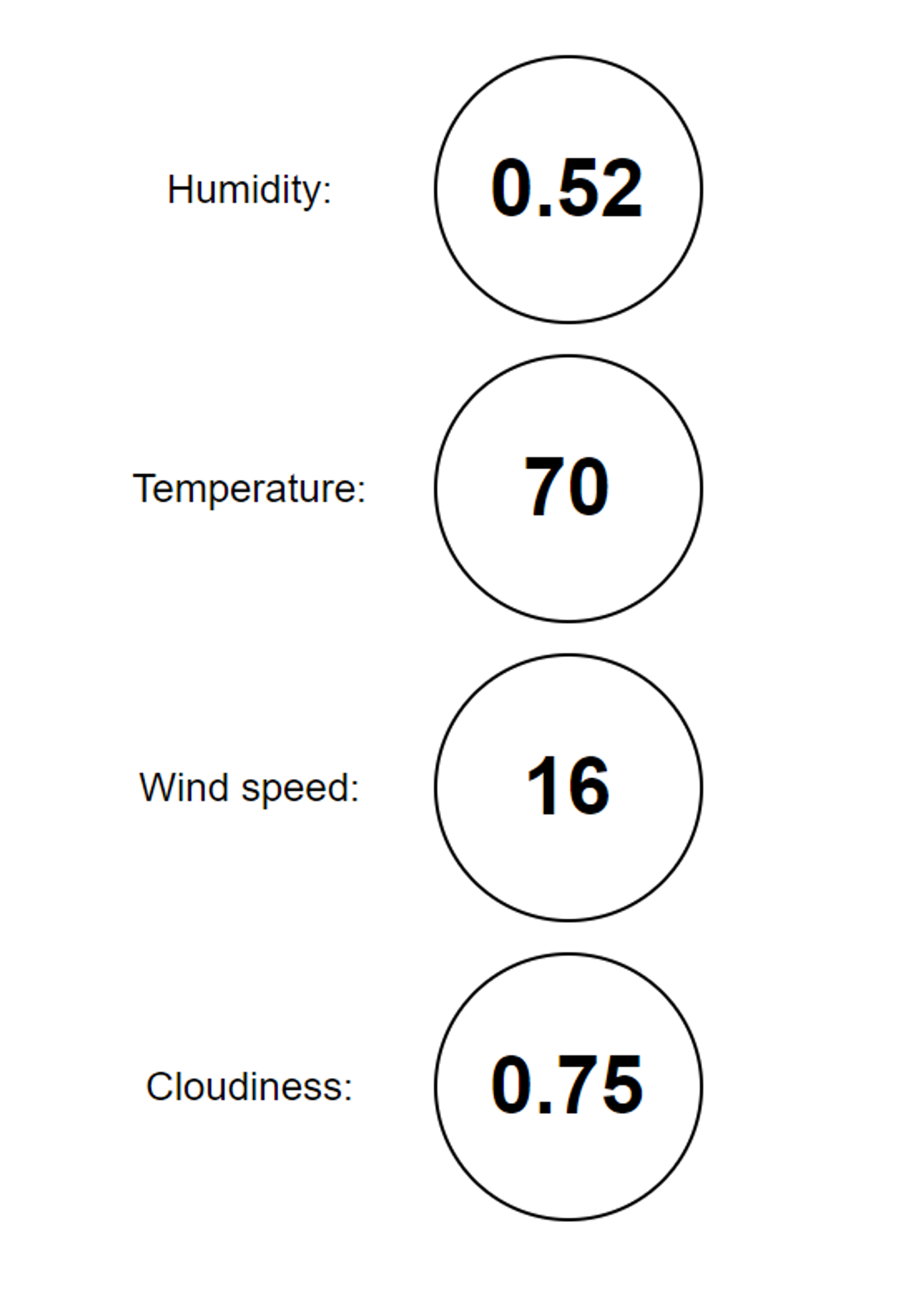
Notice how we converted “very cloudy” to 0.75 for the cloudiness value. As mentioned before, neural networks can only work with numbers, so we must encode a numerical value to each description.
The Output Layer
The output layer is similar to the input layer. Depending on what the model is predicting, there could be multiple nodes. In our instance, since we just want the model to predict whether it’s raining or not, we would only have one output node:
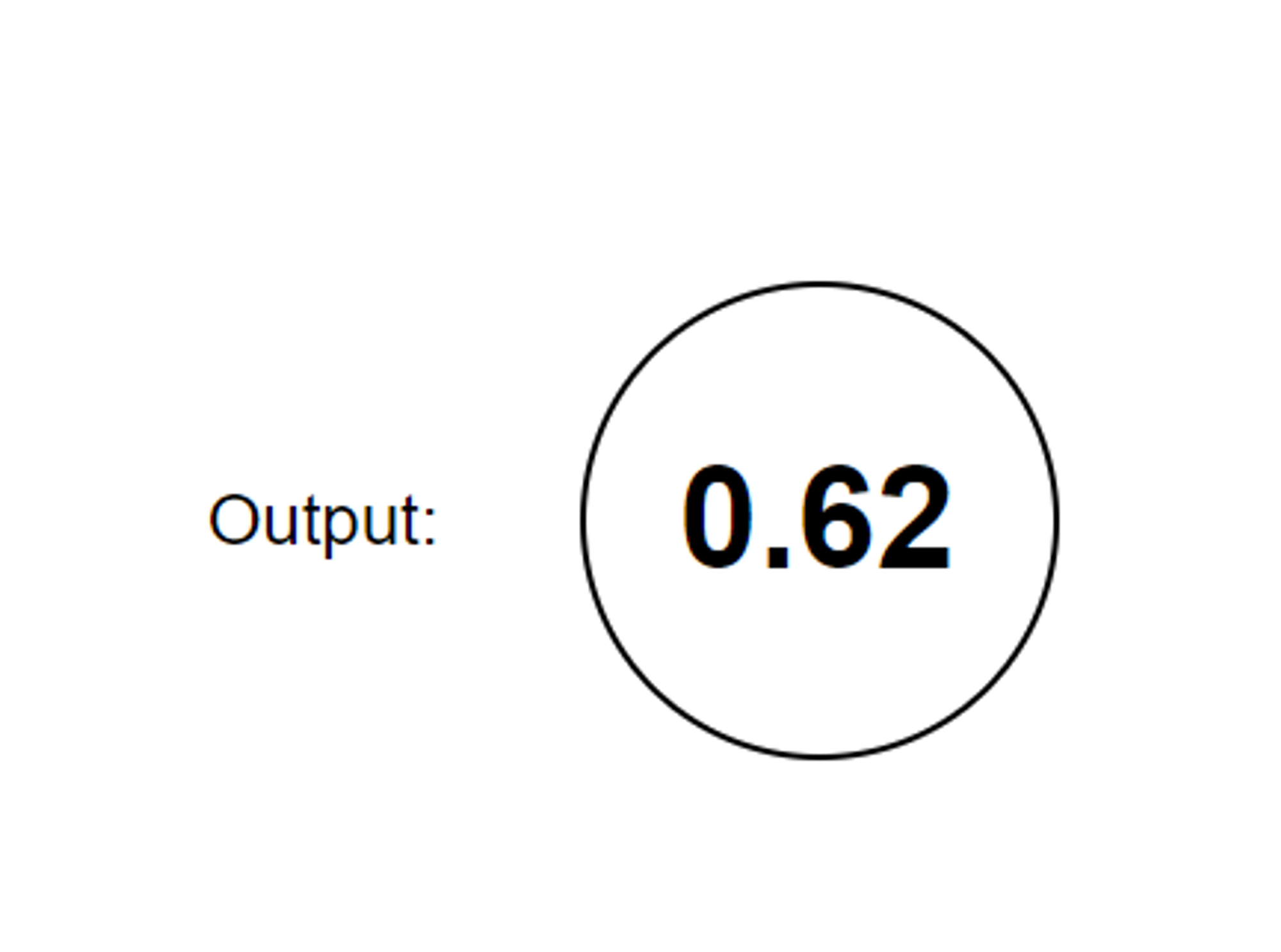
Generally, multiple outputs are used for multi-class classification, where instead of only classifying inputs into two groups, we need the model to classify input into three or more groups. For example, if we were to build a model that recognizes handwritten digits, we would need 10 output nodes, one node for each possible digit from 0 - 9.
Connections, Weights, and Biases
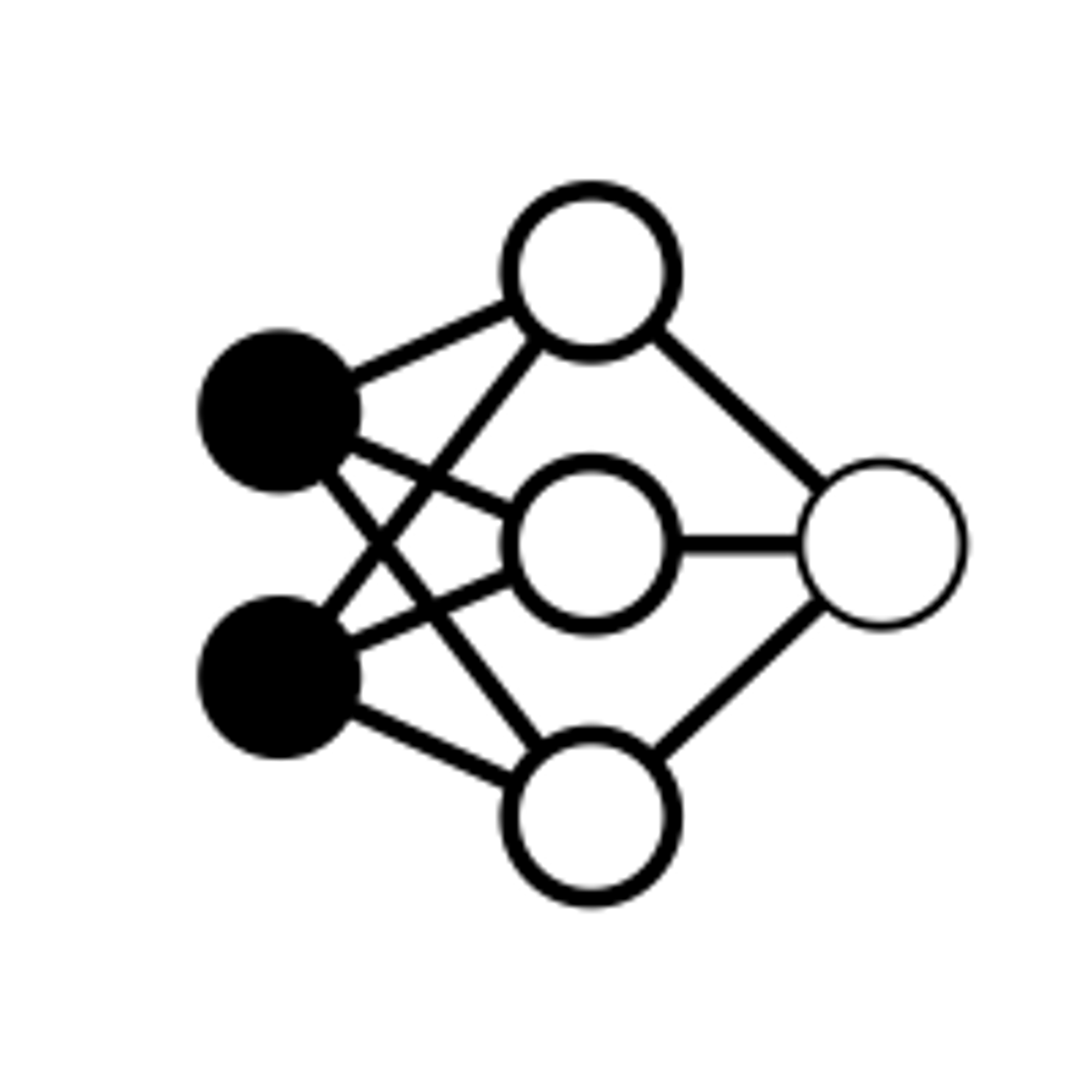
Having unconnected layers by themselves would be pretty useless, which is why we have each layer connected with the layers before and after. In a typical neural network, each node is connected to every other node in the layer before and after it. If we were just to have an input and output layer, our neural network would look like so:
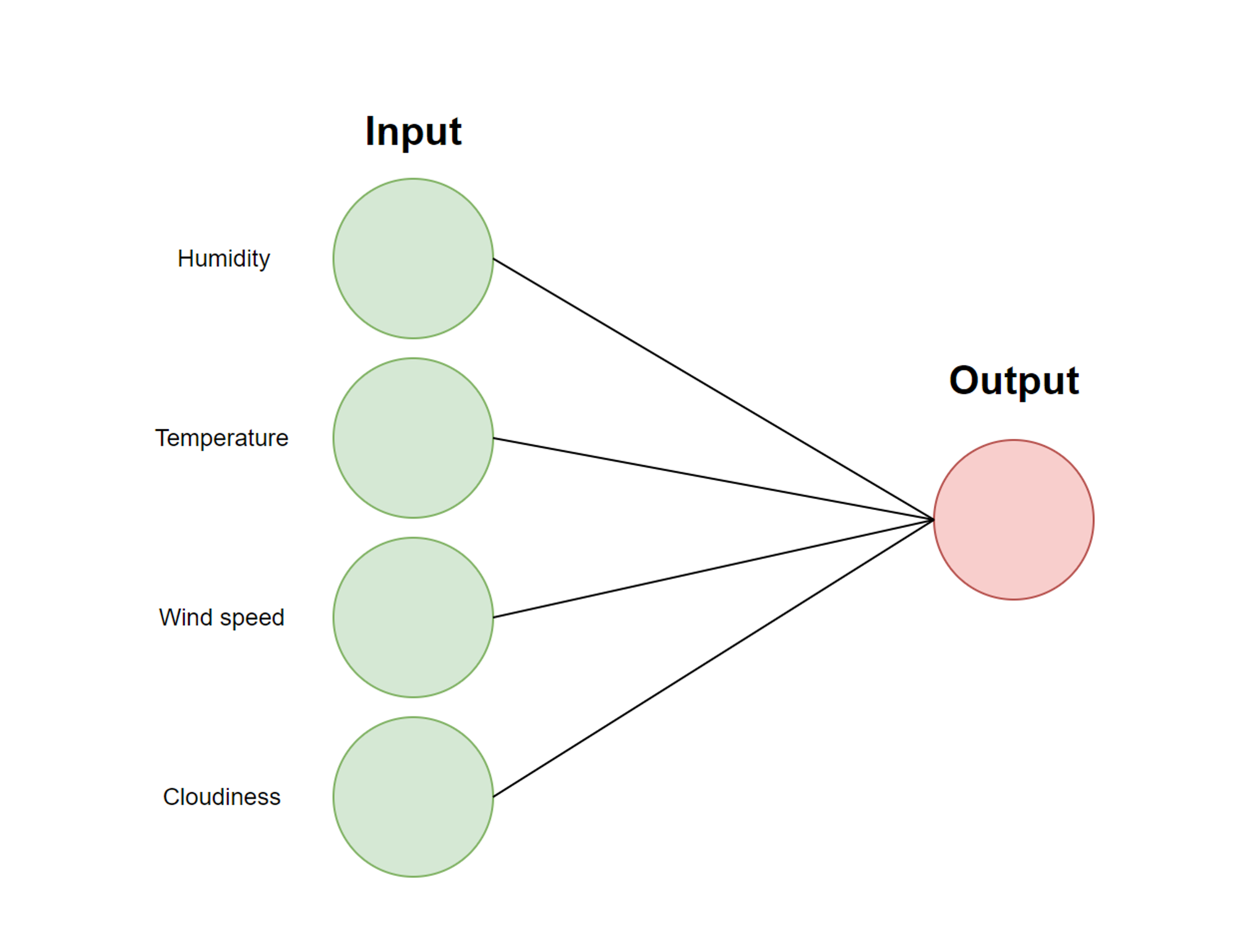
So how are numbers aggregated from layer to layer? The process is actually incredibly similar to logistic regression. Let’s label the values in each input node respectively. Since certain nodes may have more influence in whether or not it’s raining, we add a weight onto each connection between the layers, which we can label . Whenever a layer receives information from a previous layer, the values from the previous layer will be multiplied by their corresponding weight. Since each node aggregates information from all nodes in the previous later, the weighted numbers are then summed together:
Notice how we also add a constant term at the end, that’s called a bias, which just allows us to shift answers by a constant number. Represented visually, our neural network can be labelled as follows:
We aren’t done, however. After we find the weighted sum , we need to apply an activation function. One popular activation function is the sigmoid function , which is the same function used in logistic regression.
This function is popular especially in classification problems, as the sigmoid function maps inputs to outputs in the range from . Here are some of the most widely used activation functions:

Hidden Layers
Often, two layers (an input and output layer) isn’t enough for complex tasks—introducing hidden layers enables neural networks to produce more nuanced decision boundaries. Put simply, hidden layers are layers of nodes that are placed between the input and output nodes. Let’s add a hidden layer to the previous network.
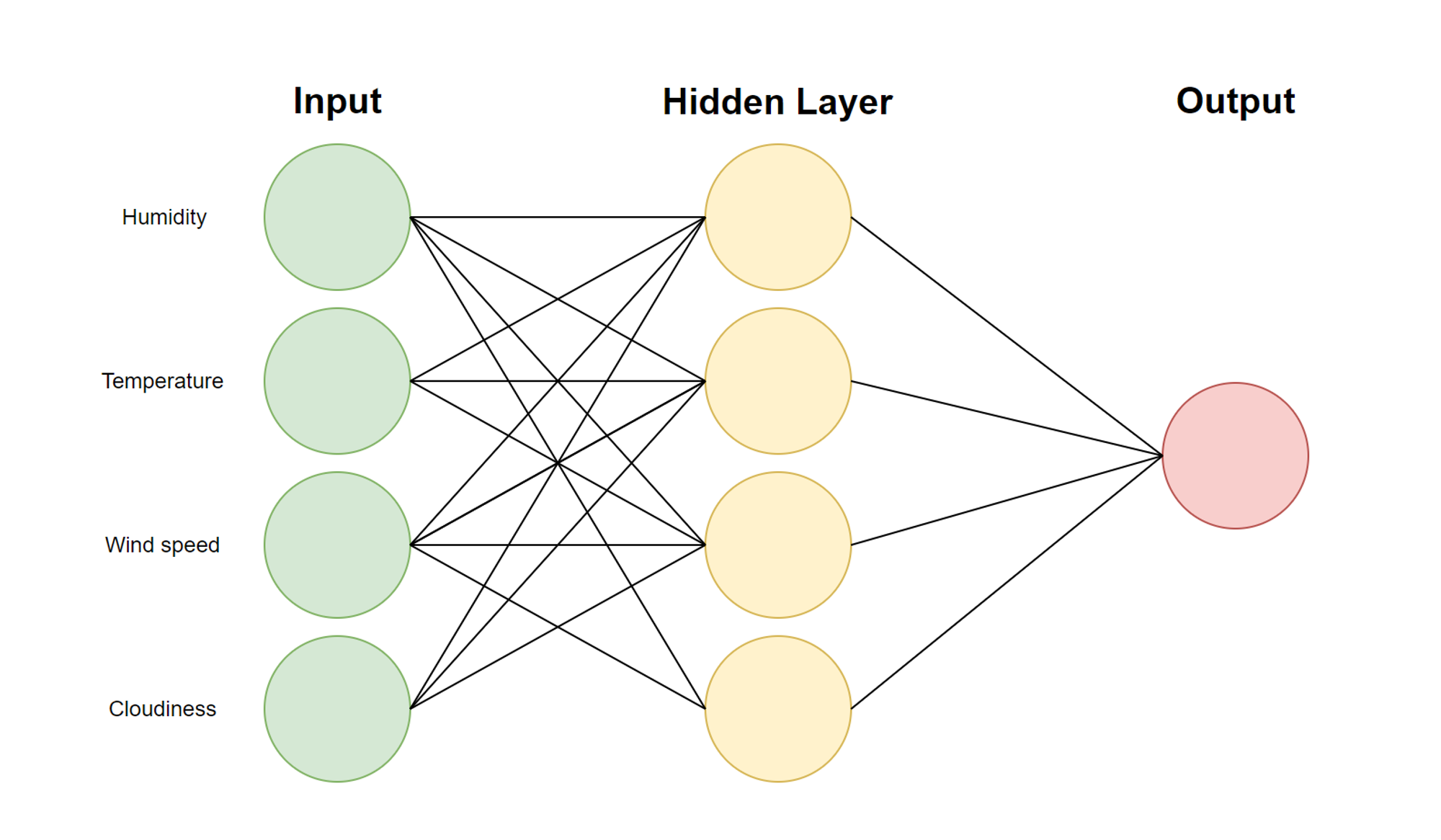
The way information flows from input to output is the same as discussed previously. Each hidden layer calculates a weighted sum from each of the inputs and applies an activation function to that weighted sum. Then, each value from the hidden layer is fed into the output, which finds another weighted sum and applies another activation function.
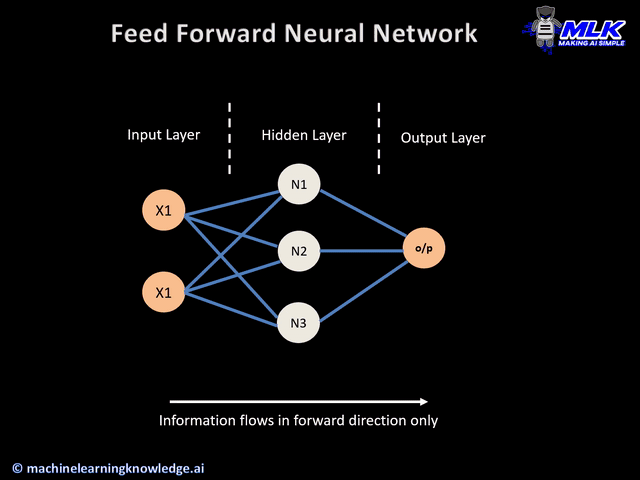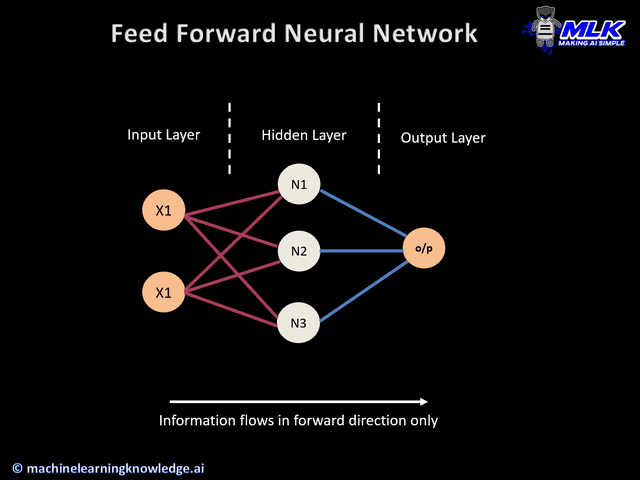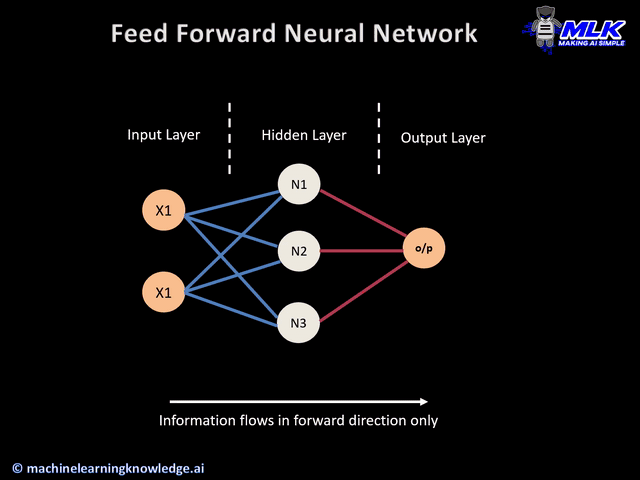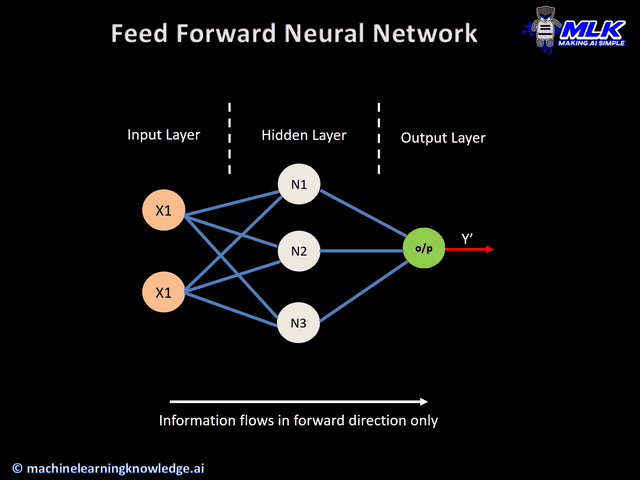
We aren’t restricted to how many hidden layers we add, or how many nodes we add to each layer—there’s a lot of room to experiment and play around. As a warning, adding too many hidden layers can lead to overfitting.
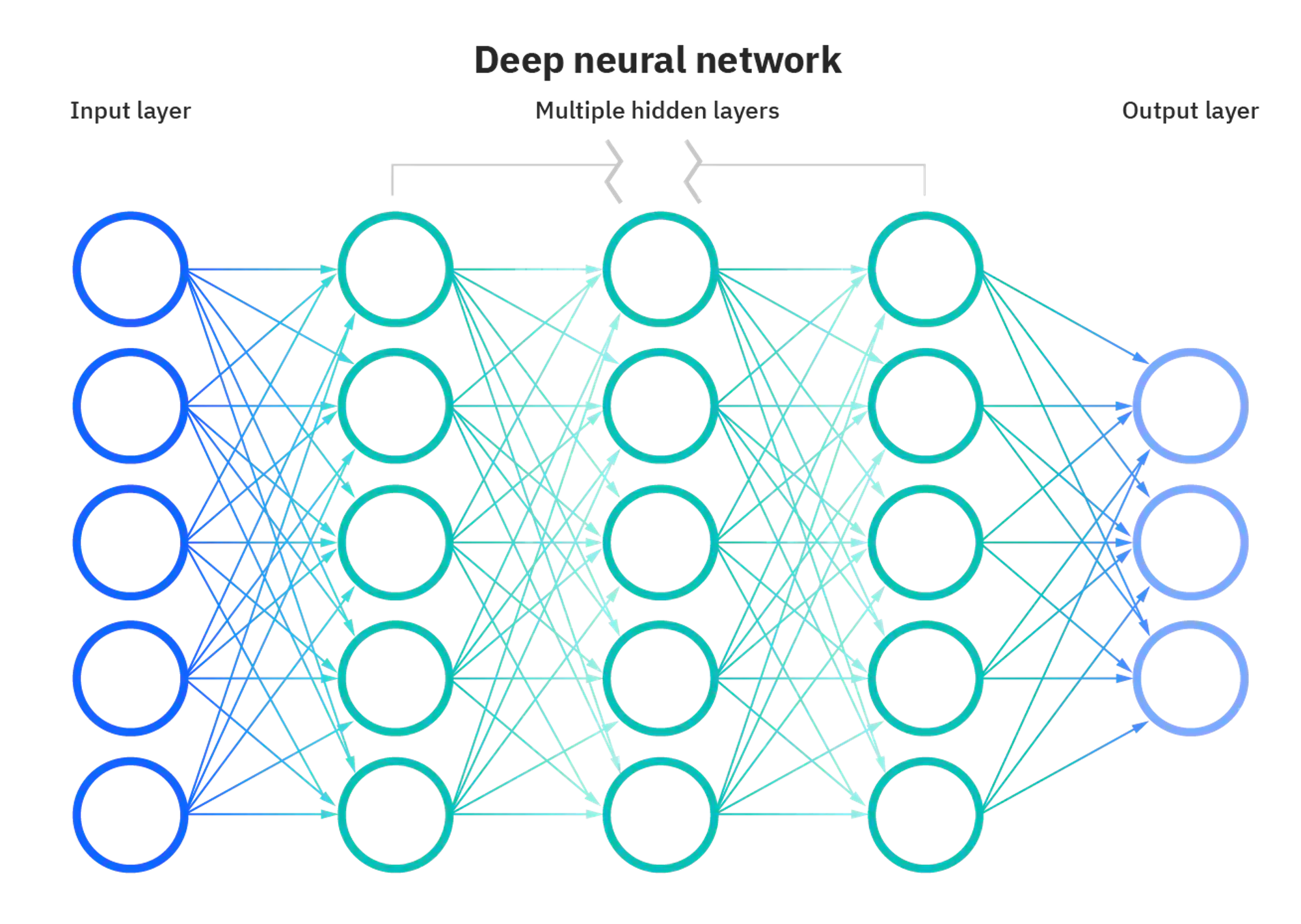
That’s pretty much it for the structure of a neural network! Refer to this image for a more generalized depiction of a neural network:
Video Resource

Copyright © 2021 Code 4 Tomorrow. All rights reserved.
The code in this course is licensed under the MIT License.
If you would like to use content from any of our courses, you must obtain our explicit written permission and provide credit. Please contact classes@code4tomorrow.org for inquiries.