Concepts
Unfortunately, Support Vector Machines are one of the most-difficult-to-explain algorithms. They employ very complex mathematical tools, especially involving probability theory and higher-dimensional state spaces. So in this section, we will only try to provide you a primer on the basic idea of Support Vector Machines. As you have probably become used to hearing by now, you don’t have to fully understand the mathematics behind the algorithm to use it to solve the problems you want to.
Classification, as we have studied it so far, is largely centered on this idea of Decision Boundaries. Finding the most efficient decision boundaries can help us differentiate between examples that belong to different classes/categories, which is our end goal. However, this tends to become difficult to do accurately, since data can sometimes appear very convoluted. In such cases, finding simple 2D curves that neatly separate classes can be close to impossible, unless you’re willing to compromise on accuracy - a lot.
The Support Vector Machine Algorithm (or SVM, as we like to call it), re-envisions this data in higher dimensions. Think about this for a second:
Imagine the most chaotic plot of data on a 2D graph. Now let’s say you’re a huge Data fan, and you’ve printed the graph onto a large piece of cloth and made that your tablecloth at home. Now if there was nothing on the table cloth, and you and a friend were to lift it up from both sides dramatically, you would see the cloth bend into a 3D curve. It’d look something like a valley, depending on how hard you pulled on it. While Gravity is otherwise not to be ignored, let’s say we could stop it for just a second. If you look at the table cloth now, the data is likely to be more separable. In particular, deforming it in this way means that you could even find a particular height, above which all examples on the cloth fall in one class, and below which they fall into the other. Isn’t that cool? Here is what this process looks like visually:
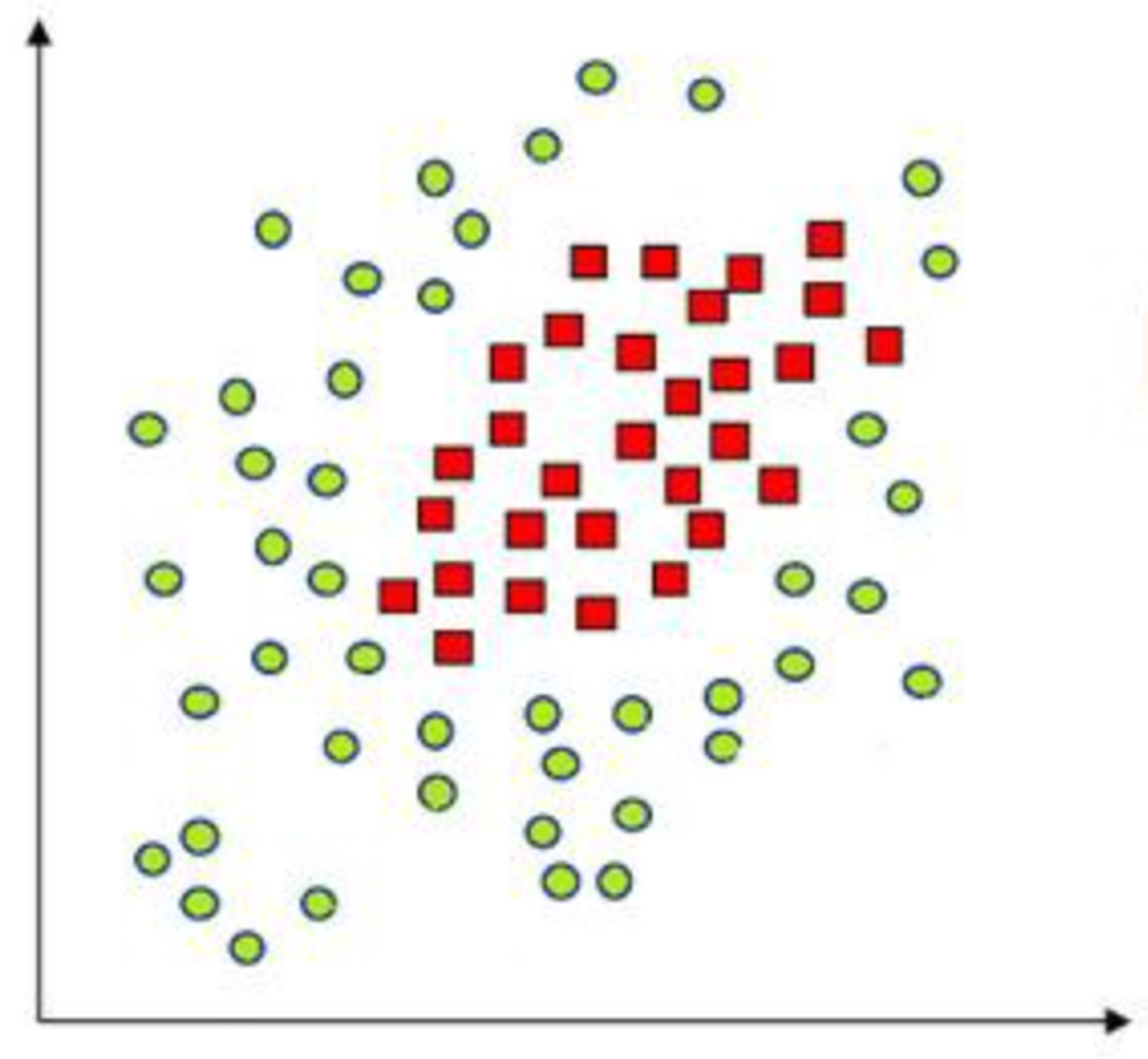
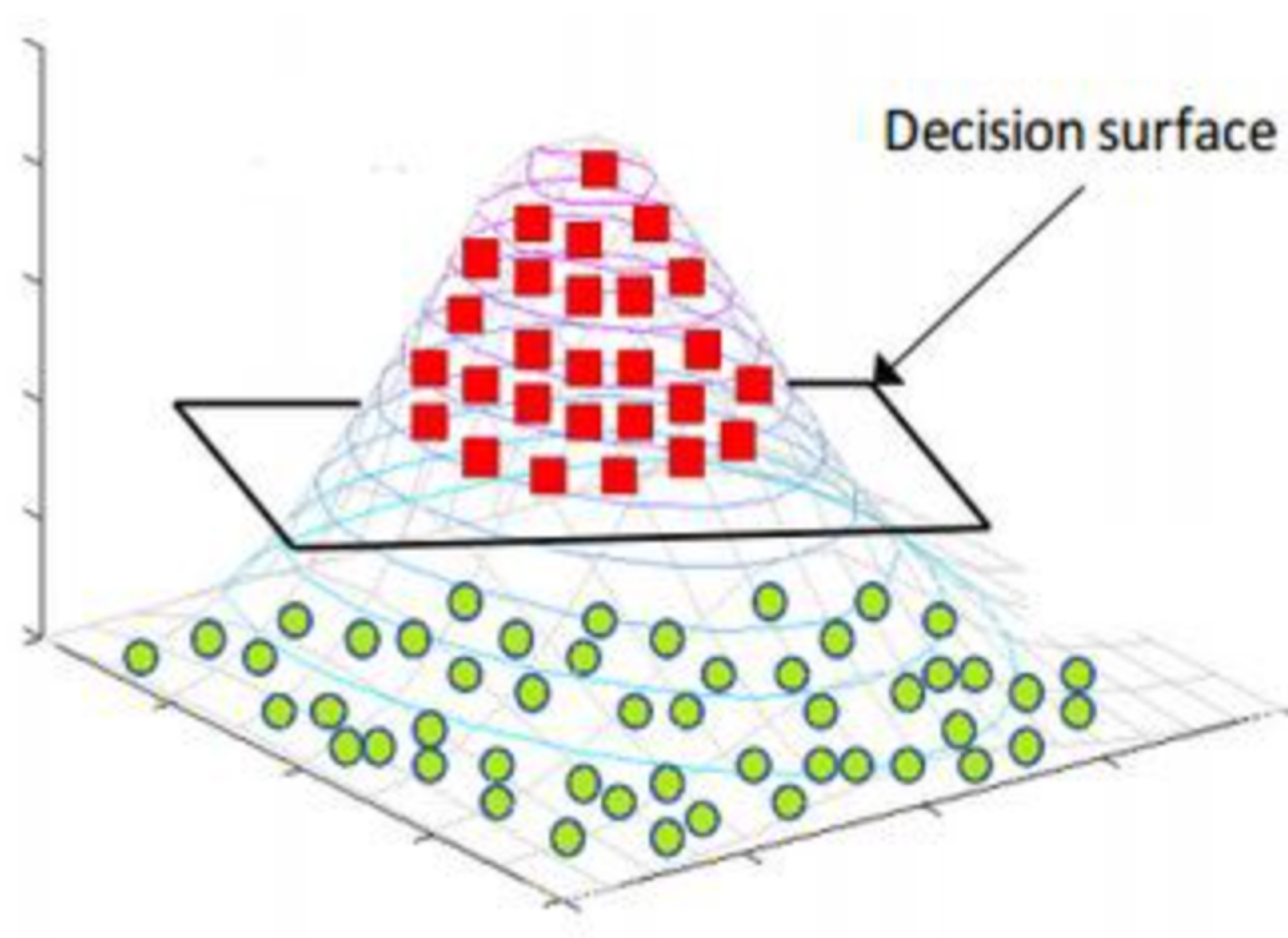
SVMs simply apply this kind of idea to much higher dimensions than merely three, which makes them all the more convenient. When they construct Higher-Dimensional Decision Boundaries, these are called HyperPlanes - since they are no longer merely lines, but planes and cubes, and so on.
Maybe if you’re interested, someday you’ll go on to learn the mathematics of this algorithm. We’ll stop with this much for now though. There are some pros and cons to applying SVM algorithms to a Machine Learning problem though, and we will close out the course by discussing these.
Previous Section
6.1 IntroductionCopyright © 2021 Code 4 Tomorrow. All rights reserved.
The code in this course is licensed under the MIT License.
If you would like to use content from any of our courses, you must obtain our explicit written permission and provide credit. Please contact classes@code4tomorrow.org for inquiries.