Now that we've begun working on Polynomial Regression, you may be thinking, is there a way to think about Polynomials Regression as Multiple Regression? Well, yes.
Formats of Multiple and Polynomial Regression
Let's consider the format of multiple regression:
and polynomial regression:
If you notice, the two look quite similar. We can make the following substitutions:
In this sense, we can think about polynomial regression as multiple regression with different features that are just various powers of the same feature. For example, if the initial feature is a length in meters, polynomial regression could use features in units of squared, cubed or quartic, meters.
However, this is not the same as Multiple Regression which could literally use features in units of meters, liters, kilograms and volts, all in the same problem.
By combining multiple regression and polynomial regression, we can then get the best of both worlds, where we can incorporate different features with different powers. The equation does get a lot more messy, but here's a gyst of what the resulting curve fit could look like for multiple dimensions:
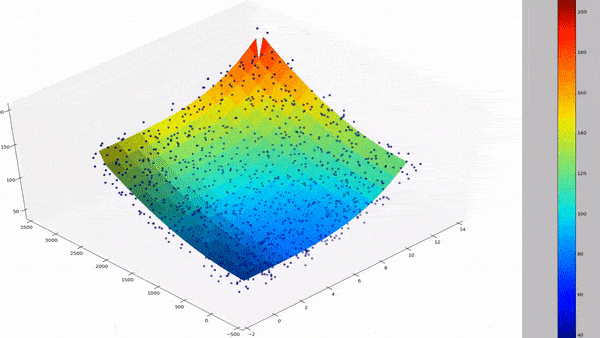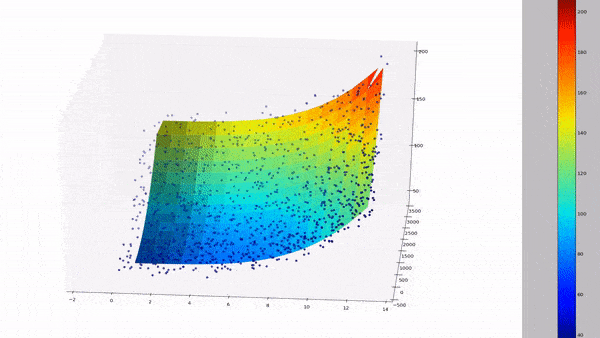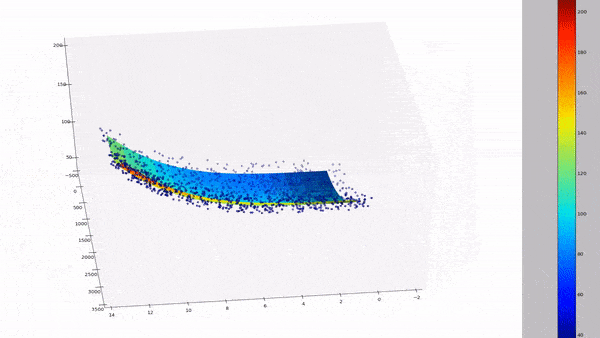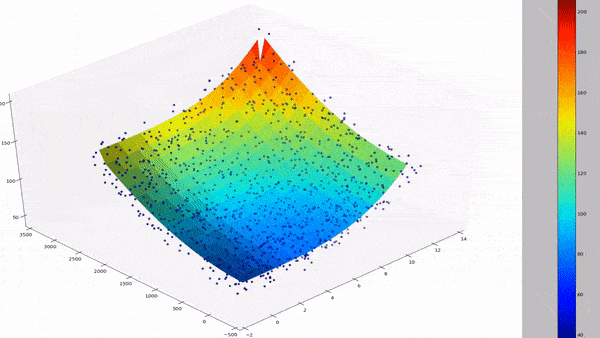
PolynomialFeatures():
Sklearn has a useful function to try out different combinations of polynomial regression, known as
PolynomialFeatures(). Let's see how to use it.The only parameter to this function is an integer n, to tell you what the maximum degree till which you want to try the combinations of polynomials. This produces a matrix that contains the features set to different degrees, and different combinations. In the next lesson, we'll discuss how we can use
PolynomialFeatures() and another function fit_transform in conjunction. Copyright © 2021 Code 4 Tomorrow. All rights reserved.
The code in this course is licensed under the MIT License.
If you would like to use content from any of our courses, you must obtain our explicit written permission and provide credit. Please contact classes@code4tomorrow.org for inquiries.